Importance of goal setting in financial planning

You may have observed in limited over cricket that teams with strong batting line-up choose to bowl first after winning the toss. The reason is obvious; when you are batting second you know, exactly how much, you have to score to win the match. You can calculate your required run rate and decide the batting order accordingly. In other words, if you have a clear target, decision making becomes easy. In financial planning, if you have clear quantitative goals then planning process becomes simpler and much more effective.

Let us understand how this works with the help of a simple example. Suppose you are saving to make the down payment for a house. Let us assume you want to make a down-payment of Rs 20 lakhs in 3 years. If you expect to get 10% p.a. return on investment, then you can calculate how much to save every month, so that you can meet your down-payment goal. All you have to do is use a simple Microsoft Excel formula, PMT. The PMT formula has 5 arguments in the order in which they are listed.

• Rate of return


• Number of Periods


• Present Value of your savings


• Future Value of your savings


• Type (0 or 1); 0 if investment is made at the end of each period and 1 if investment is made at the beginning of each period

Let us understand now how to use the formula in the example above.

• Rate of Return:

  You are expecting 10% annual returns. Since you will save on a monthly basis, you will have to convert the annual returns into monthly returns. How? You simply divide the annual returns by 12. So your Rate of Return will be 10%/12 or 0.8333%



• Number of Periods:

  You plan to make the down-payment after 3 years. However, since you plan to save monthly, you will again have to convert the annual period into a monthly period, by multiplying 3 with 12 or 36 months



• Present value of your savings:

  Since you do not have any savings at present for the house, this will be zero.



• Future value of your savings:

  You want to save Rs 20 lakhs in 3 years. So the future value of your savings should be 20,00,000 if you want to meet your goal.



• Type (0 or 1):

  You have to select 0 or 1, depending on whether you want to make the investments at the beginning of every month or end of every month. Let us assume that, you want to make the investments at the beginning of every month. You should select 1.

The formula with all the arguments is shown in the box below

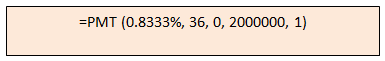
Once you enter the formula in a spreadsheet, Excel will calculate how much you have to save every month. In this case, the answer is -47,472. Please note the sign is negative because it is your cash outflow.

Just because you know the answer it does not mean your problem is solved, but it can help you make important decisions. Let us start with the easiest decision. If you can comfortably save Rs 47,472 every month for your house purchase, then you are in a happy position. You can evaluate, whether you can shorten the time period by saving a bit more; you may be able to purchase the house at a lower cost, if you can make the down-payment earlier.

Let us now discuss the more difficult situation, where you cannot afford to save Rs 47,472 every month. In such a situation, you have two choices. You can either reduce your goal from Rs 20 lakhs to a lower amount or wait longer till you have enough savings to buy the house. How will you make a decision whether you lower the goal or lengthen the time to reach the goal?

Let us first share a cricketing analogy. Ideally, most captains want to bowl first because he has a clear target for the team, when they are batting second. However, they may not have that luxury. For instance, if the captain loses the toss and is put in to bat, he does not have a choice. Even if the captain wins the toss, if he fears that the pitch will deteriorate as the game progresses, he may decide to bat first. If there is possibility of rain later in the match, then there may be advantage for team batting first (Duckworth Lewis Rule has historically favoured teams batting first). There may be a variety of reasons for batting first, but the biggest disadvantage is that, you do not know, exactly how much run you need to win the match. The other disadvantage is that, the captain of the team batting first does not know how the pitch will behave until the batsmen have faced sufficient number of overs (the team batting second have much more knowledge when they come out to bat).

Armchair critics should appreciate how difficult the job of a cricket captain is. However, as an investor your job is less difficult. In cricket, there are only two outcomes that matter at the end, winning or losing. Fortunately, as an investor you have multiple options. Let us now go back to our previous example and discuss what decision you will make, if you are not in a position to save the adequate amount needed to meet your goal.

Let us recap the example. You need Rs 20 lakhs to make the down-payment for a house in 3 years. At expected 10% return on investment, you need to save Rs 47,472 per month to meet your goal. But given your income and expenditure, you cannot save Rs 47,472 every month. What will you do?

Let us first discuss, what the captain of the team batting first, will instruct his opening batsmen to do. He will instruct them to score as much as they can, without taking undue risks. Similarly, in the investment example, you will have to determine the maximum amount you can save for the house down-payment without compromising other financial goals. Make a careful expenses of your income and expenses, see where you can reduce your expenses and estimate the maximum amount you can save for this goal. I have seen that, people are usually very conservative when they are trying to estimate, the maximum can save. You should not be conservative. Try to save the maximum amount and savings will become a habit. Let us assume that, you can save a maximum amount of Rs 30,000 per month for the house purchase. Now you can make some important decisions, but before that, you should evaluate two alternative scenarios:-

• The maximum you will be able accumulate in 3 years at your maximum savings rate


• The time it will take you to meet your Rs 20 lakhs goal at your maximum savings rate

Let us discuss the first scenario. How much will you be able to accumulate in 3 years? You can use Microsoft Excel formula FV to calculate the amount. The FV formula has 5 arguments in the order in which they are listed.

• Rate of return


• Number of Periods


• Savings in each period


• Present value of your savings


• Type (0 or 1); 0 if investment is made at the end of each period and 1 if investment is made at the beginning of each period

Note the similarities between the FV formula and the PMT formula discussed earlier. Let us understand now how to use the formula in the example above.

• Rate of Return:

  You are expecting 10% annual returns. On a monthly basis, your Rate of Return will be 10%/12 or 0.8333%



• Number of Periods:

  You plan to make the down-payment after 3 years. The number of monthly periods therefore can be calculated by multiplying 3 with 12 or 36 months



• Savings in each period:

  You can save maximum Rs 30,000 per month. You should note that, this should be entered in the FV formula with a negative sign because it a cash out-flow for you



• Present value of your savings:

  Since you do not have any savings at present for the house, this will be zero



• Type (0 or 1):

  You have to select 0 or 1, depending on whether you want to make the investments at the beginning of every month or end of every month; in our case the beginning of every month and hence 1

The formula with all the arguments is shown in the box below.

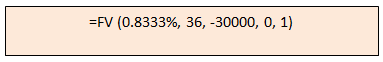
Once you enter the formula in a spreadsheet, Excel will calculate how much you will accumulate at the end of 3 years. The answer is Rs 12.63 lakhs. You should set your and family’s expectations accordingly. If your dream home required a Rs 20 lakhs down-payment and you have Rs 12 – 13 lakhs, you and your family are likely to be disappointed, but if you set expectations objectively then the emotional impact is much less.

Reducing your ambition is not the only option available to you. Philosophers say that, time solves a lot of problems. Time is not merely a philosophical concept; it is a very important concept in finance and investing. In the above example, if you can wait longer, you may be able to afford your dream home. How long do you have to wait? You can use Microsoft Excel formula NPER to calculate the waiting period. The NPER formula has 5 arguments in the order in which they are listed.

• Rate of return


• Savings in each period


• Present value of your savings


• Future Value of your savings


• Type (0 or 1); 0 if investment is made at the end of each period and 1 if investment is made at the beginning of each period

Note the similarities between the NPER, FV and PMT formulae discussed earlier. Let us understand now how to use the NPER formula in the example above.

• Rate of Return:

  You are expecting 10% annual returns. On a monthly basis, your Rate of Return will be 10%/12 or 0.8333%



• Savings in each period:

  You can save maximum Rs 30,000 per month. You should note that, this should be entered in the FV formula with a negative sign because it a cash out-flow for you



• Present value of your savings:

  Since you do not have any savings at present for the house, this will be zero



• Future value of your savings:

  You want to save Rs 20 lakhs in 3 years. So the future value of your savings should be 20,00,000 if you want to meet your goal.



• Type (0 or 1):

  You have to select 0 or 1, depending on whether you want to make the investments at the beginning of every month or end of every month; in our case the beginning of every month and hence 1

The formula with all the arguments is shown in the box below.

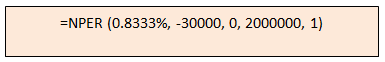
Once you enter the formula in a spreadsheet, Excel will calculate in how much time you will accumulate Rs 20 lakhs. The answer is 53 months (around 4.5 years). The price of your desired property may have appreciated in the extended period; so you should allow some more time, but you can see that, you will be able to meet your goal if you are prepared to wait longer. Whether you reduce the scale of your ambition or wait longer for your ambition to be fulfilled is your personal decision, but once you have a clear goal, your chances to meeting it are much higher.

Conclusion

The dream of every cricketer is to play for India, but only a handful makes it to the national team. It is not that, the cricketers who did not make it to the highest level were not talented; some may even have been more talented than test cricketers. Harsha Bhogle, the celebrated commentator, once said in a corporate event that I was fortunate to be part of, focus is key differentiator for success. The same applies to personal finance success. Focus means having a goal and working towards it. Once you have a goal and are committed to it, chances of success increases exponentially.

Disclaimer: An Investor education and Awareness initiative of Aditya Birla Sun Life Mutual Fund.