Duration is one of the most important concepts of fixed income investments. Bond prices have an inverse relationship with interest rate changes; bond prices go up when interest rate falls and vice versa. Duration is a measure of the sensitivity of a bond’s price to interest rate changes. There are two analytical measures of bond duration – Macaulay Duration and Modified Duration.
Macaulay Duration: Bonds pay interest (technically known as coupon) at regular frequencies and the principal amount (face value of the bond) upon maturity. Macaulay Duration is the weighted average time (number of years) an investor has to remain invested, till the present values of the cash-flows received from the bond equal the price paid for the bond. Bond maturity is one of the most important factors affecting Macaulay Duration – longer the maturity, longer the Macaulay Duration. The Macaulay Duration of a bond which pays coupons will always be less than the bond maturity.
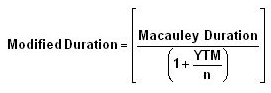
Modified Duration: Modified duration is the percentage change in a bond’s price to 100 bps change in interest rates. We need to know (calculate) Macaulay Duration of a bond to calculate the Modified Duration.
In this formula YTM is the yield to maturity and n is the number of coupon payments made in a year. If Modified Duration of a bond is 7 years, then 1% fall in interest rates will cause the bond’s price to rise by 7%. If Modified Duration of a bond is 3 years, then 1% rise in interest rates will cause the bond’s price to fall by 3%.
In summary, duration is a measure of interest rate risk of a bond. If you have low appetite for interest rate risk, you should invest in short duration debt mutual funds which have less interest rate risks. If you have high risk appetite, you can invest in long duration debt mutual funds.